How much does the Earth really weigh? The answer has divided scientists

Calculating the mass of the Earth is a difficult task. The planet contains everything from rocks and minerals to millions of species of living things, and is covered with countless natural and man-made structures. So scientists say there is no clear and precise answer to the question of how much the Earth weighs.

In astronomy, the mass of the Earth is used as a non-systematic unit of mass. It is approximately equal to 5.97219 × 10 to the 24th power of kg. The Live Science publication talked about attempts to determine the weight of the Earth and disputes between scientists.

What is the mass of the Earth?

According to NASA, the mass of the Earth is 5.97219 × 10 to the 24th power of kg. This is equal to about 13 quadrillion times the mass of the Egyptian pyramid of Chephren, which itself weighs about 4.8 billion kg. The mass of the Earth fluctuates slightly due to the addition of space dust and gases escaping from the atmosphere, but these tiny changes will not affect the Earth for billions of years.

The force of gravity

Physicists still do not agree on decimals, and it was not easy to get a preliminary total mass value. Since it is impossible to scale the Earth, scientists had to triangulate its mass using other measurable objects.

Stefan Schlamminger, a metrologist at the U.S. National Institute of Standards and Technology, said that scientists were primarily guided by Isaac Newton's law of gravity. Everything that has mass also has a force of attraction, meaning that any two objects will always have a certain force between them.

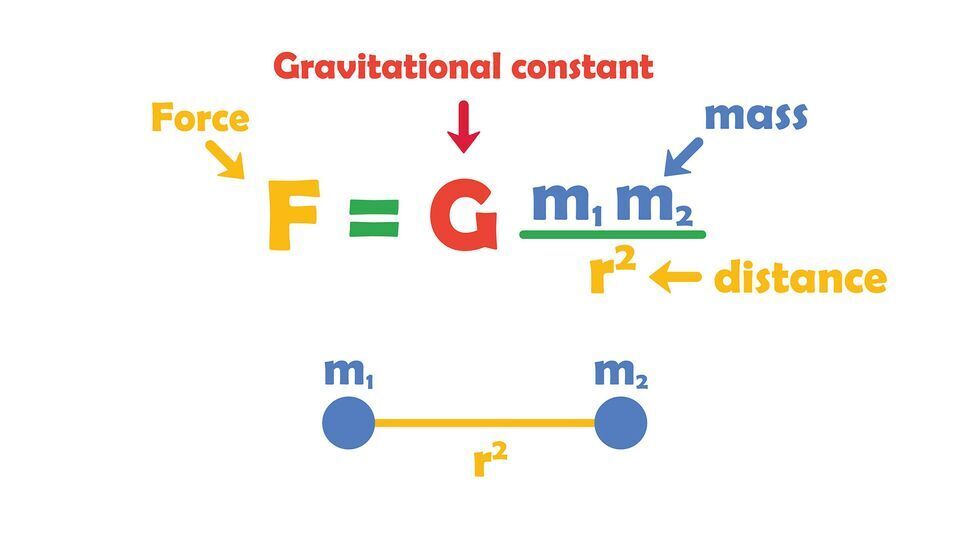
Newton's law of gravitation states that the force of attraction between two objects (F) can be determined by multiplying the respective masses of the objects (m₁ and m₂), dividing them by the square of the distance between the centers of the objects (r²), and then multiplying this number by the gravitational constant (G), also known as the intrinsic force of gravity, or F=G((m₁*m₂)/r²).

Using this equation, scientists could theoretically measure the mass of the Earth by measuring the force of the planet's gravity on an object on the Earth's surface. But there was a problem: no one could find a number for G.

Cavendish experiments

In 1797, physicist Henry Cavendish began what became known as the Cavendish experiments. Using an object called a torsion balance, consisting of two rotating rods with lead spheres attached to them, Cavendish found the amount of gravity between the two sets by measuring the angle on the rods, which changed when the smaller spheres were attracted to the larger ones.

"His work was very original and had a lot of influence at the time," said John West, a physiologist at the University of California, San Diego.

Knowing the mass and distance between the balls, Cavendish calculated that G = 6.74 × 10-11 m3 kg-1 s-2. The International Research Council's Data Committee now lists G as 6.67430 x 10-11 m3 kg-1 s-2, which is only a few decimal places off from Cavendish's original number. Since then, scientists have used G to calculate the mass of the Earth using other objects of known mass and arrived at the number 5.97219 × 10 to 24 powers of kg that we know today.

Despite the fact that more than two centuries have passed since Cavendish's experiment, his method of torsional equilibrium is still in use today. Schlamminger emphasized, however, that while Newton's equations and torsional weights are important tools, the measurements they provide remain subject to human error. Over the centuries since Cavendish's experiments, various scientists have measured G dozens of times, and each has obtained a slightly different result. The numbers differ by only a thousandth of a decimal place, but that's enough to change the calculation of the Earth's mass and cause controversy among scientists.

Subscribe to OBOZ.UA channels in Telegram and Viber to keep up with the latest events.